Mire ezt a cikket a kezében tartja a kedves olvasó, addigra már javában elkezdődött a tavaszi szorgalmi időszak. A vizsgák közepette nem sok idő szokott jutni bárminemű kikapcsolódásra, de ha esetleg mégis összejön, akkor az legalább legyen tartalmas és szórakoztató. A kínálat ismét széleskörű volt.
Egy keveset töprengtem azon, hogy a szakomnak megfelelő biológia és orvostudomány-orientált előadások mellett most talán tényleg kicsit ki tudna kapcsolni, vagy legalábbis más irányba tudná terelni a gondolataimat egy más jellegű előadás vagy szimpózium. Nem kellett sokat keresgélni, ugyanis a vizsgák ellenére sok helyütt zajlanak az előadássorozatok, amelyekben a szünetet mindössze az ünnepek jelentették. S így esett a választásom az év 2., de a szezon 9. Atomcsill előadására, január 26-án Szabó György tolmácsolásában, amely A játékelmélet kölcsönhatásának anatómiája címet viselte.
Dr. Szabó György
Jelenleg a Magyar Tudományos Akadémia Energiatudományi Kutatóközpont (MTA-EK) Műszaki fizikai és anyagtudományi Intézetének munkatársa. 1996-ban szerezte meg PhD fokozatát, 2007-től pedig az MTA köztestülete rendes taggá választotta. Jelenlegi foglalkozása tudományos tanácsadó és a Komplex Rendszerek csoport vezetője, emellett számos tudományos közlemény szerzője. Kutatási témái és érdeklődési köre az önszerveződő mintázatok, az Ising-típusú modellek és az evolúciós játékelmélet. Ezekből a témákból kaphattunk egy kis ízelítőt a Professzor úr előadásában.
Bejelentés
A performansz a nagy hagyománynak örvendő, az előző előadással kapcsolatos totókiosztást és egy kisebb előadást követően kezdődött el. A főelőadás felkonferálása előtt Dr. Tél Tamás egyetemi tanár, a Fizika doktori iskola vezetője pár szót mondott a tanárképzésről, az oktatási innovációkról és perspektívákról a nyílt nap(ok) apropóján. 2013 óta van újfajta tanárképzés, aminek keretein belül az úgynevezett szakpárképzésekre való jelentkezés lehetséges. A képzés elején van egy kötelező alkalmassági beszélgetés, amely Tél tanár úr elmondása szerint egy rendkívül könnyed beszélgetés az oktatók és a hallgatók (leendő tanárok) között, amelynek az a célja, hogy felszínre kerüljenek a hallgatók különböző motivációi, céljai. A tantervben nincs szakdolgozat a 3. év után, hiszen egy egységes 5 éves, osztatlan képzésről van szó. Az utolsó év már a rezidens oktatás jegyében telik, ami már a tanári életpálya része. A többéves felkészítés alatt nagyon nagy hangsúlyt fektetnek a pedagógiai és a pszichológiai készségek kiépítésére és fejlesztésére. Ahogy a professzor úr mondta: A tanár híd a kutatás és a társadalom között, ezért esszenciális a szerepe. Az utolsó pár szóban még azt is megtudhattuk, hogy a tanárképzéshez illeszkedik egy doktori képzés is, minden évben sikeres és kalandos gólyatáborokat szerveznek, van Mikulás est és hasonló, pezsgő közösségi élet. Ha esetleg az olvasók között van olyan, akinek tervbe van véve a tanári pálya választása és esetleg hezitált, akkor hadd szolgáljon ez a fentebbi kis szösszenet egyfajta pozitív megerősítésként. Az esetleges érdeklődőktől pedig bármilyen kérdéssel lehet ezen az e-mail címen tájékozódni: tel@general.elte.hu.
Az előadás
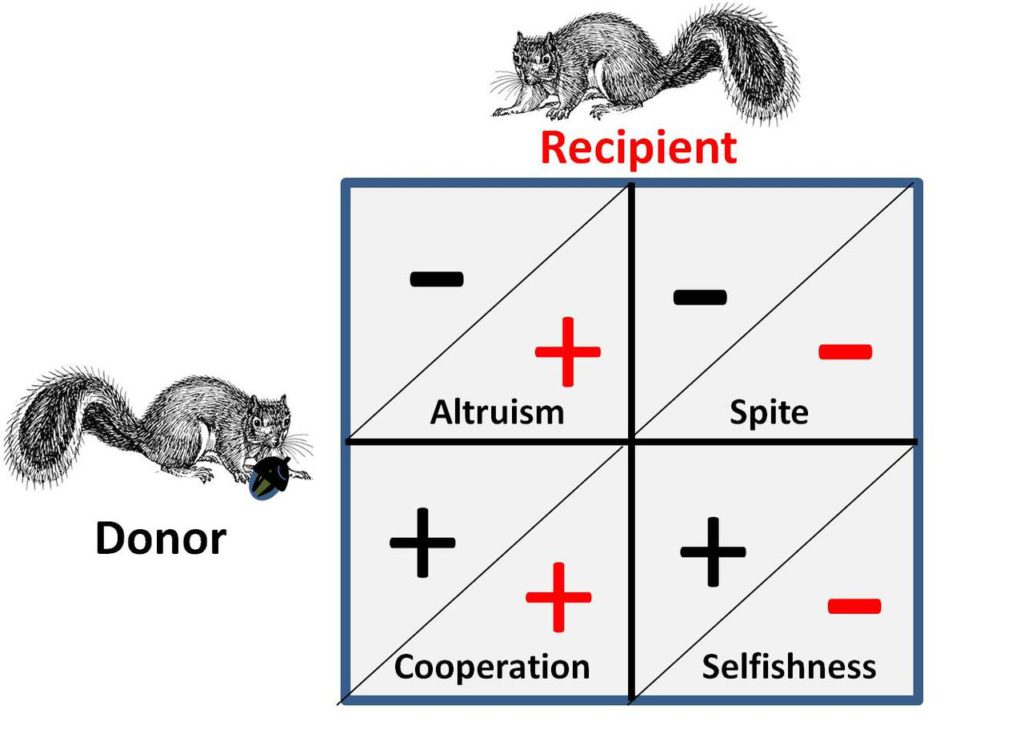
A rövidke felszólalás után Dr. Cserti József felkonferálta volt oktatóját, aki – elmondása szerint – nagyban meghatározta az érdeklődését a szilárdtestfizikai pályán. A fő téma az evolúciós játékelmélet volt, amit egy rendkívül összeszedett, jól strukturált matematikai-fizikai aspektusból kaptunk meg. Az első témakör a párkölcsönhatás és mátrixok viszonya volt. A nyitásban felmerült egy frappáns kérdés, amelyet maga az előadó fogalmazott meg: De mégis hogy jön a szilárdtestfizika mindehhez? Nos, a szilárdtestfizikai kísérletek egy része áttehető evolúciós szintre. S ez itt a kulcs! Az atomok helyettesíthetők vírusokkal, baktériumokkal, soksejtű élőlényekkel (emberekkel) és a köztük létrejövő makroszkopikus interakciókkal, amelyek vizsgálata bizonyos pontokon hasonló. Ennek alapja a Neumann-féle játékelmélet, ami az interperszonális reakciókat leírja. Ám, ebben a darwinista evolúciós dinamika is közrejátszik, aminek köszönhetően egy sokszereplős evolúciós rendszer jön létre, amely dinamikusan fejlődik.
Annak érdekében, hogy a téma a látszólag egyszerű elemektől az egyre bonyolultabbak felé menjen, először egy kétstratégiás evolúciós játékelméleti modell lett bemutatva egy négyzetrácson. Ekkor a játékosok egy LxL-es négyzetrács x pontjain helyezkednek el. A magasabb nyeremény reményében változtathatják a stratégiájukat. A matematikai jelölés akkor válik egyszerűvé, ha egységvektorokat jelölünk. A biológiai játékelmélet rendszerekben a játékos lehet az imént említett mikroorganizmusok egyike vagy akár az ember. Stratégiának tekinthető (bármelyik élőlényre vagy vírusra vonatkozóan) az, hogy mutáns vagy nem mutáns (vad típusú), ragadozó vagy zsákmány, tisztességes vagy élősködő. Ennek fizikai analógiája lehet például, hogy egy kristályfelületen van-e atom vagy nincs, a mágneses momentuma (spin) felfelé áll vagy lefelé; egy tetszőleges vegyületben van-e szabad elektron vagy nincs. Az úgynevezett nyereménymátrix határozza meg x játékos tényleges hasznát. Ez egy négyparaméteres modell. Számos mennyiségi rokon fogalmat és párhuzamot találhatunk a fizikai mikrovilág és az evolúciós makroszkópikus rendszerek között. A kölcsönhatás mindig az adott játékos állapotára vonatkozik. Az összes elemzésnél a szimmetrikus játékokra korlátozzák a számításokat. Ha a játékosok stratégiát cserélnek, akkor a nyereményük is cserélődik. Ha a négyzetrácson véletlenszerűen kiválasztott játékos megegyezik egy másik játékos értékével, akkor az egy mindenki számára ideális állapotot feltételez. Ki lehet számolni az n-stratégiás játékosok nyereményének a valószínűségét, amelyre sok dinamikai szabály vonatkozik. Ebből egyet kell alkalmazni, ráadásul súlyozottan. Ez a rendszer az élővilágra vonatkozóan pont úgy viselkedik, mint az élettelen anyag tekintetében. További paraméterezés során kell elkülöníteni a két rendszer vizsgálatát egymástól. Ilyenkor bevezetésre kerül az Ising-modell, amelyben ferromágneses rend alakul ki. Véletlen kezdőfeltételből indulunk el, de beáll a ferromágneses állapot alacsony hőmérsékleten. Ennek analógiája egy közérthető példán: gyakran merül fel a kérdés a kezdő számítógép-felhasználók körében, hogy Linuxot vagy Windows-t telepítsenek-e. Ebben a helyzetben ideális állapothoz közelít az a szituáció, hogy megnézem azt, hogy a szomszédom mit telepít, ugyanis akkor tudunk egymásnak segíteni (ez egyfajta csordaszellem hasonlat). De mi van, ha a szomszéd nem ért hozzá, csak ő is követett valakit/valamit? Ekkor további paraméterek ismerete szükséges. A modell grafikus ábrázolása engem a pszichológiában gyakran alkalmazott Rorschach tintafolt-tesztre emlékeztetett. Ennek a rendszernek a fizikai analógiája az adott felületen való atomkiválás és monoréteg képződés valószínűsége. A további játékok bemutatásánál terítékre került a koordinációs játék, amelynek típusos példája a személyi jövedelemadó (SZJA). Ekkor a fő kérdés, hogy az ismerős mit választ(hat)? Előbb-utóbb az adminisztrációban érvényesül az elektronikus bevallás preferenciája. Ekkor egy antikoordinációs (antiferromágneses) eset keletkezhet, azaz az ellentettjét csináljuk annak, mint a másik személy. Erre talán még közérthetőbb példa az, amikor két ember egy étterem keskeny ajtajában állnak s ki szeretnének jutni. Az ajtón kimenni egyszerre nem jó. Ha egyik sem megy ki, az sem jó. Ekkor a megoldás a társadalmi vonatkozásban is hasznos preferenciasorrend felállítása. Nő-férfi esetben már adott protokoll is meg van írva, s az udvarias személyek ehhez ragaszkodnak is (ismeretlen helyre a férfi megy be, de kifelé mindig a hölgyeket kell előreengedni). Ha a fizikai oldalát nézzük, akkor a rendszer nem tud belefejlődni az optimális állapotba (ahol senkinek nem éri meg stratégiát változtatni, tehát mindenki a legjobb állapotában van, nincs optimálisabb állapot) és létrejön egy egyensúly.
A következő témakör már a többparaméteres mátrixokról szólt. Itt le lett szögezve, hogy a játékelméletben az átlagnyereménynek nincs értelme. A kétstratégiás játék elemi összetevői egy nagy A mátrix összetevőire bontva felírható. Az egyes mátrixok elemi jelentése az az irány, amely megmutatja, hogy mi történik, ha az adott stratégiát választják. A másik lehetőség a koordinátarendszer elemeinek elforgatása négydimenziós paramétertérben. Ha grafikusan új bázisvektorokat és -mátrixokat szeretnénk létrehozni, akkor a Descartes koordinátarendszerben lévő egységvektorokat el kell forgatnunk egy bizonyos phi-szöggel. A forgatással és a vektorok skaláris szorzatával kapott összeg új, ún. ortogonális bázisvektorok (bázismátrixok). A bázismátrixok által definiált elemi játékok közé tartozik a konstans játék (irreleváns tag), amely csupa 1-es értéket tartalmazó mátrix, a koordinációs játék, amelyben a nyeremény csak önmagunktól függ, s van olyan játék is, ahol a nyeremény mástól is függ. Az 1-dimenzió nem mutatja a ferromágnesességet, amiből kifolyólag a német fizikus, Enrst Ising otthagyta a fizika tudományát. Viszont 2- és 3-dimenzióban viszont megmagyarázza a ferromágnes létezését és a fázisátalakulásokat. Miután a pályaelhagyó tudós elmenekült az Egyesült Államokba (a világháború idején nem kívánatos személy volt zsidó származása miatt), sok év után, egy ottani egyetemen derült ki számára, hogy mindenki ismeri a nevét, ugyanis a kudarcnak ítélt leírását használták a mérések és kutatások alapjának, amivel leírták a további dimenziók ferromágneses állapotot.
A 2-, 3- és n-stratégiás játékok komponensekre bontása meghatározott szempontok szerint történhet. Ilyenkor a szimmetriákat keresik és az alapokat definiálják, amiből kiindulva bonthatnak. Kiválasztunk egy n-dimenziós teret kifejező egységvektort, amihez definiálunk egy Descartes elemi mátrixot. Kapunk egy diadikus szorzatot, ami megmutatja, hogy a mátrix adott i-edik sorának, j-edik eleme milyen értéket vesz fel. A potenciál egyenes arányban van a stratégiaprofillal, ami viszont a nyeremény értékével. Létezik 9 dimenziós paramétertér, amiből 5-nél nincs kölcsönhatás. A szimmetrikus összetevők alkotják a koordinációs játékokat. A szimmetrikus nyereménymátrix következményei lehetnek, hogy a két játékos nyereménye azonos, az egyéni érdek pedig egyenlő a közösségi érdekkel. Ez egy dilemma nélküli társadalomhoz vezetne – ami sajnos erősen idealisztikus megközelítés. Lehetséges az is, hogy az i*, j*-ot kiválasztjuk, amik a mátrix legnagyobb elemei. Ezek azonosak a fizikai rendszerek alapállapotával. Ha a kettő egyenlő, akkor mindenki az egyik stratégiát választotta.
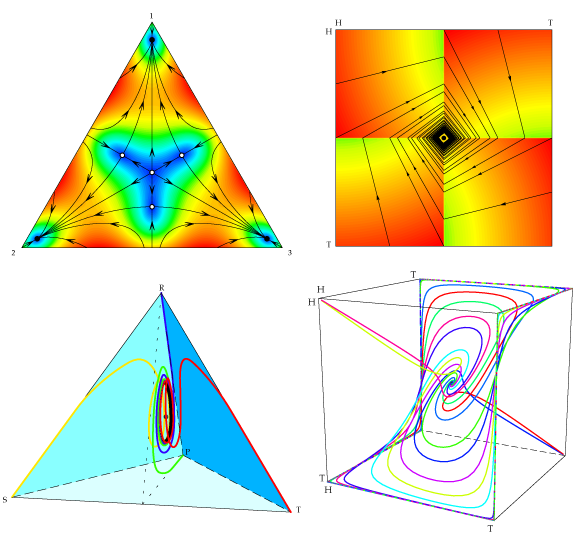
Egy antiszimmetrikus bázismátrix ciklikus dominanciát alakít ki. Ilyen a kő-papír-olló játék, amelyben prioritási sorrendek vannak definiálva, az alábbiak szerint kő<papír<olló<kő… A váltások során az aktív játékos mindig nyer, s emellett 6 darab pozitív számnak az összege nem lehet zérus. Ezért nincs potenciál a rendszerben. Ez makroszkopikusan egy kevert Nash-egyensúlyhoz vezet, ami sok stratégia együttlétezését jelenti (biodiverzitás).
Az előadás végéhez közeledve a kölcsönhatások összefonódásáról, illetve ezek fontosságáról volt szó. Számomra külön öröm volt, hogy az egyes stratégiák bemutatásakor egy igényes kitekintést kaptunk a biológiai és a társadalmi rendszerekbe is. Ezek megvitatása után kicsit könnyebb bele- és mögé látni ezeknek a helyzeteknek. Megérteni nem egyszerű, de úgy érzem, hogy az ilyen előadások látogatása mindig egy lépéssel közelebb visz a kollektív tudáshoz.
Zárásképp egy kis kedvcsináló a tavaszi félévi előadásokhoz. A lista korántsem teljes és egyes helyeken az időpontok is változhatnak, így megkérdek minden kedves Olvasót, hogy tájékozódjanak a megfelelő médiumokból:
- Február 23. Pipek Orsolya: Mit tehet a fizikus a rákkutatásért? (Atomcsill)
- Március 08. III. Élettudományi Liftbeszéd Fesztivál
- Március 09. Budapest Science Meetup
Remélem, hogy sikerült mindenkinek kipihenni magát, hogy újult erővel vágjon bele a félév kihívásaiba. Szerencsés félévkezdést kívánok!